Assim, perceba que no cálculo da tangente de um ângulo na circunferência trigonométrica não é vantajoso usar o mesmo triângulo retângulo que usamos para o cálculo do seno e do cosseno desse ângulo. Nesse caso, devemos trabalhar com um triângulo semelhante a este, de forma que o cateto adjacente tenha a medida do raio da circunferência, ou seja, 1 unidade.
Para encontrarmos esse triângulo semelhante desejado, traçamos um novo eixo (em vermelho na figura abaixo), tangente à circunferência e paralelo ao eixo y, passando pelo ponto A, que é considerado o ponto de origem dos arcos. Por convenção, chamamos esse novo eixo de eixo t. Considere um arco AM e o triângulo retângulo OMN, formado a partir da projeção da extremidade do arco (ponto M) nos eixos x e y:
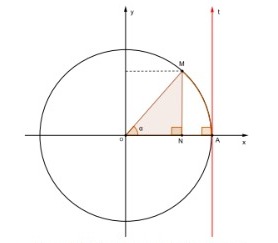
Figura 95: Eixo t, tangente à circunferência.
Veja que basta estender a hipotenusa do triângulo OMN, até que ela “corte” o novo eixo no ponto T, para encontrarmos o triângulo semelhante desejado:
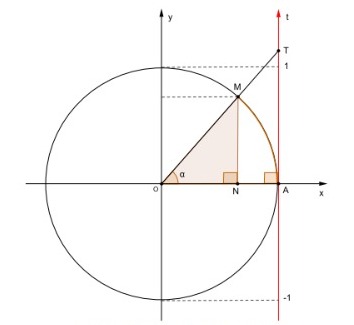
Figura 96: Prolongamento de OM até o eixo t.
BAIXAR O LIVRO EM PDF