Com os conceitos de ângulo e triângulo, podemos entrar, a partir de agora, nos estudos mais específicos de trigonometria. Você se lembra do que dissemos lá no início sobre do que trata a trigonometria? É preciso sempre ter isso em mente: a trigonometria estuda as relações entre as medidas de lados e ângulos de um triângulo.
E esse estudo se dá estabelecendo-se tais relações a partir do triângulo retângulo.
Em um triângulo retângulo é possível estabelecer seis razões trigonométricas, considerando-se seus lados. Certamente você está se perguntando: Como assim, razões trigonométricas? Calma, já vamos entender melhor o que significa isso.
Quando estabelecemos uma divisão entre duas quantidades ou duas grandezas (grandeza é tudo aquilo que pode ser medido), estamos comparando-as entre si, tomando uma delas como unidade de comparação. Ou seja, estamos dizendo “quantas vezes uma cabe na outra” ou, em outras palavras, “quanto uma é maior ou menor do que a outra”. O número expresso por essa divisão (o resultado da operação) chamamos de razão. Nesse sentido, dizer que "seis dividido por dois é três", por exemplo, significa dizer que "seis é três vezes maior do que dois", ou ainda, que "seis é o triplo de dois". Ou seja, a razão entre seis e dois é três!
Logo, quando dizemos que em um triângulo retângulo é possível estabelecer razões trigonométricas, considerando-se seus lados, isso significa que é possível estabelecer razões (divisões) entre as medidas de seus lados. Por exemplo, na figura abaixo, temos um triângulo retângulo com lados medindo 10 cm, 8 cm e 6 cm.
Calculamos duas possíveis razões entre seus lados:
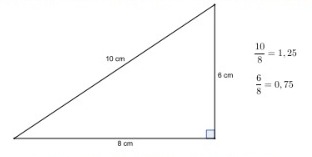
Figura 22: Algumas razões entre as medidas de lados
de um triângulo.