Com isso, já temos tudo o que precisamos para o cálculo das razões trigonométricas. Observe que o cateto oposto a α é o lado BD, o cateto adjacente a α é o lado OD e a hipotenusa é o lado OB, que mede 1, já que é o raio unitário da circunferência trigonométrica:
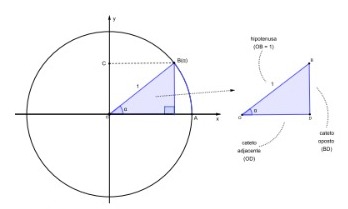
Figura 84: Triângulo retângulo associado a um arco AB em uma
circunferência trigonométrica e seus catetos em relação ao ângulo α.
Ora, se, como vimos, o seno de um ângulo é a razão entre o cateto oposto e a hipotenusa, e, como na circunferência trigonométrica a hipotenusa do triângulo retângulo associado a um arco sempre mede 1, então, na circunferência trigonométrica, o seno de um ângulo α sempre será equivalente à medida do cateto oposto desse triângulo; já o cosseno de um ângulo α sempre será equivalente à medida do cateto adjacente desse triângulo.
Percebeu a facilidade quanto aos cálculos, dada pela convenção de se tomar a circunferência com raio unitário?
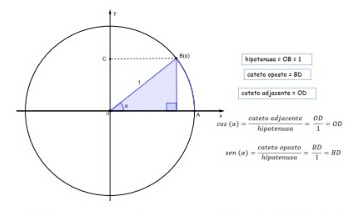
Figura 85: Razões seno e cosseno no triângulo retângulo associado
a um arco AB na circunferência trigonométrica.
