Agora observe o triângulo retângulo associado ao arco EF na circunferência trigonométrica. Veja que o ângulo α indicado tem medida de 60° (180° - 120°).
A hipotenusa é o segmento de reta que liga o centro da circunferência à extremidade do arco (ponto F), e tem a medida do raio: 1 unidade. O cateto adjacente ao ângulo de 60° nesse triângulo tem medida igual ao valor da coordenada x do ponto F (projeção ortogonal de F no eixo x), que é -0,5. Note que o sinal é negativo pois seguimos a orientação do sistema de coordenadas [Efetivamente, uma medida não possui valor negativo. Estamos dizendo aqui que a medida do cateto assume valor negativo apenas em referência à sua posição na circunferência trigonométrica, cujos eixos são orientados. O mesmo acontece nos demais exemplos]. Por sua vez, o cateto oposto ao ângulo de 60° nesse triângulo tem medida igual ao valor da coordenada y do ponto F (projeção ortogonal de F no eixo y), que é 0,87.
Vamos a mais um exemplo. Considere o arco GH de medida 225° e o triângulo retângulo associado a ele na circunferência trigonométrica:
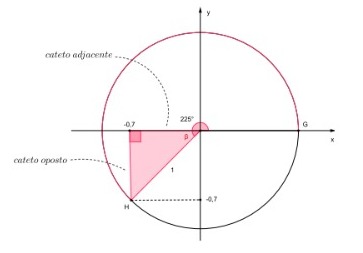Figura 75: Triângulo retângulo a partir de um arco GH^
de medida igual a 225° e projeção do ponto H, nos eixos x e y.
BAIXAR O LIVRO EM PDF