Ou seja, ser semelhante significa que um dos triângulos é uma ampliação ou uma redução do outro. Em outras palavras, se através de um “zoom” pudermos colocar um triângulo sobre o outro, de forma que eles fiquem exatamente sobrepostos, temos então dois triângulos semelhantes. Isso vale não apenas para triângulos, mas para qualquer figura!
É por isso que os triângulos das figuras 30 e 31 são semelhantes. Veja que seus ângulos têm medidas comuns e a razão entre os seus lados correspondentes é sempre a mesma. Se calcularmos a razão entre as hipotenusas encontramos o valor 2. Esse mesmo valor é encontrado ao calcularmos as razões entre os catetos opostos e entre os catetos adjacentes. Então, dizemos que a razão de semelhança entre os dois triângulos é 2, ou seja, o triângulo maior é o dobro do triângulo menor.
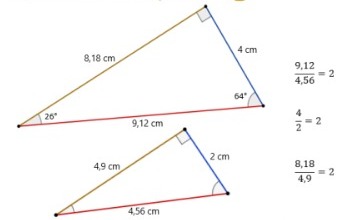
Figura 32: Razão entre os lados correspondentes
de dois triângulos
Mas tem mais! Também a razão entre dois lados de um mesmo triângulo será igual à razão entre os lados correspondentes de um triângulo semelhante a ele. Considere os triângulos semelhantes do exemplo abaixo. Veja que as razões entre os lados de cada triângulo têm o mesmo valor:
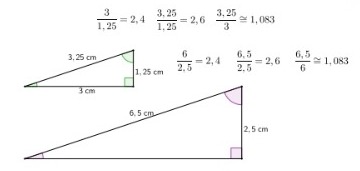
Figura 33: Razão entre lados de dois triângulos semelhantes.