Logo, em um triângulo sempre temos três ângulos internos e três ângulos externos. Além do uso de letras gregas para dar nome a ângulos (assim como indicamos na seção anterior), pode-se denotar os ângulos de um triângulo (ou de qualquer polígono) pela letra correspondente ao seu vértice sobreposta por um acento circunflexo. Em um triângulo de vértices KLM, por exemplo, podemos denotar os ângulos por Kˆ, Lˆ e M. [Podemos também denotar os ângulos externos por Kˆ, Lˆ e Mˆ. Mas, nesse caso, para não haver confusão, há que se fazer a indicação: ângulo externo Kˆ , ângulo externo Lˆ, ângulo externo Mˆ.]

Figura 16: Triângulo KLM e seus ângulos internos.
Além disso, a soma das medidas dos três ângulos internos de um triângulo é sempre 180°. Por exemplo, se um dos ângulos internos de um triângulo mede
84° e outro de seus ângulos internos mede 65°, então seu terceiro ângulo interno, necessariamente, medirá 31°, já que a soma desses três ângulos deve medir 180°.
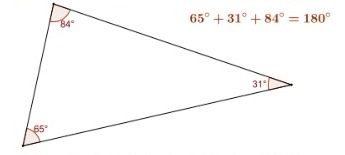
Figura 17: Soma dos ângulos internos de um triângulo.
Mas não é só isso! Os triângulos podem receber nomes específicos, a depender da medida dos seus ângulos internos. Um triângulo bastante conhecido é o triângulo retângulo. Você provavelmente já ouviu falar dele! O triângulo retângulo é aquele que possui um ângulo reto dentre seus ângulos internos. Destacamos alguns triângulos retângulos abaixo:
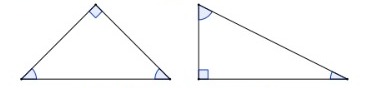
Figura 18: Exemplos de triângulos retângulos.