Dizemos, então, que A = (2,1). Assim, todo ponto no plano cartesiano é representado pelo par (x,y), em que x é o valor de sua abscissa e y é o valor de sua ordenada. O mesmo vale para a localização de todos os outros pontos indicados na figura.
Quando associamos, portanto, uma circunferência de raio unitário a um sistema de coordenadas cartesianas, de forma que a origem do sistema cartesiano coincide com o centro da circunferência, temos uma circunferência trigonométrica (que também fica dividida em quatro quadrantes, ordenados em sentido anti-horário).
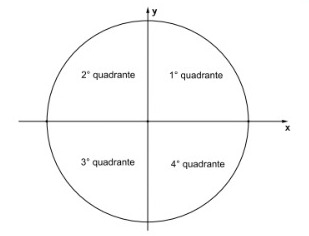
Figura 66: Quadrantes da circunferência trigonométrica.
BAIXAR O LIVRO EM PDF