Veja que a primeira razão estabelece a comparação entre a hipotenusa e o cateto maior, e o resultado significa que a hipotenusa é 1,25 vezes (ou 25%) maior do que o cateto em questão. Já a segunda razão estabelece a comparação entre o cateto menor e o cateto maior, significando que a medida do cateto menor equivale a 0,75 vezes (ou 75%) da medida do cateto maior.
É fazendo todas as comparações possíveis entre os lados de um triângulo retângulo que estabelecemos as razões trigonométricas. Vejamos como isso se dá.
Como sabemos, em um triângulo retângulo seus lados se distinguem entre hipotenusa, cateto oposto e cateto adjacente, considerando-se um de seus ângulos agudos.
Nos exemplos abaixo, consideremos o ângulo α indicado. Podemos estabelecer a razão entre o cateto oposto e a hipotenusa. Essa razão recebe o nome de seno do ângulo alpha, também denotado por sen(α):
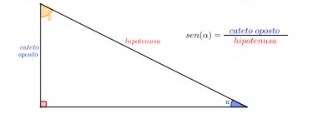
Figura 23: Razão seno de um ângulo alpha.
Outra possível razão dá-se entre o cateto adjacente e a hipotenusa. Essa razão é chamada de cosseno do ângulo alpha, ou simplesmente cos(α):
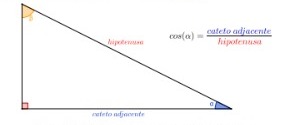
Figura 24: Razão cosseno de um ângulo alpha.