Destacamos a seguir outro exemplo. Considere o arco CD de medida 70° e o triângulo retângulo associado a ele no círculo trigonométrico:
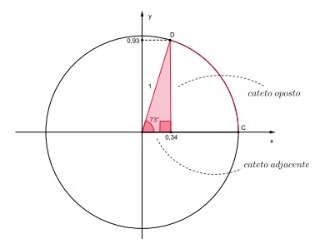Figura 73: Triângulo retângulo a partir de um arco CD^ de medida
igual a 70° e projeção do ponto D, nos eixos x e y.
Novamente, a hipotenusa é o segmento de reta que liga o centro da circunferência à extremidade do arco (ponto D) e seu valor é a medida do raio, portanto, 1 unidade. O cateto adjacente ao ângulo de 70° nesse triângulo tem medida igual ao valor da coordenada x do ponto D (projeção ortogonal de D no eixo x), que é 0,34. De maneira análoga, o cateto oposto ao ângulo de 70° nesse triângulo tem medida igual ao valor da coordenada y do ponto D (projeção ortogonal de D no eixo y), que é 0,93.
Podemos, assim, associar a qualquer arco na circunferência trigonométrica um triângulo retângulo. É isso que nos permite calcular as razões trigonométricas de ângulos de quaisquer medidas. Logo chegaremos a elas! Antes, vejamos mais alguns exemplos de arcos na circunferência trigonométrica e os triângulos retângulos a eles associados.
BAIXAR O LIVRO EM PDF