O que chamamos de regra de três simples, assim, nada mais é do que o uso dessa regularidade, ou seja, da igualdade entre o “produto cruzado” dos termos de duas razões equivalentes. Isso nos ajuda em situações em que conhecemos o valor de alguns desses termos e precisamos descobrir o valor de outro, desconhecido. É exatamente assim que convertemos medidas de ângulo em graus para radianos e vice-versa. Apresentamos a seguir alguns exemplos:
Converter de graus para radianos e vice-versa
Exemplo 1: Como determinar 140° em radianos.
Sabemos que 180° = π rad. Desejamos saber a quantos radianos (valor desconhecido) equivalem 140°.
Chamando esse valor desconhecido de x, podemos estabelecer a seguinte relação:
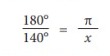
Há aí uma equivalência entre razões. Disso, sabemos que o "produto cruzado" (ou “multiplicação em x”) dos termos das razões deve resultar em um mesmo valor.
Do que temos:
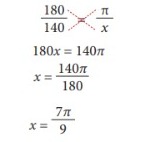
Portanto, convertendo-se a medida do ângulo de 140° em radianos, obtém-se a medida de 7π/9 rad. Ou seja, 140° = 7π/9 rad.
Exemplo 2: Determinar 2π/3 rad em graus.
Assim como fizemos no exemplo anterior, estabelecemos a seguinte relação:
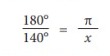
Do que temos:
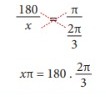
Logo,
