Perceba que, diferentemente das razões seno e cosseno, que têm valores variando entre -1 e 1, a razão tangente pode assumir qualquer valor. Isso porque, a razão tangente é definida como a razão entre o cateto oposto e o cateto adjacente de um triângulo retângulo. Uma vez que os catetos podem ter quaisquer medidas, o valor da tangente não fica limitado a nenhum intervalo.
Além disso, é importante destacar que existem ângulos que não admitem valor para tangente. Como vimos anteriormente, a tangente de um ângulo também pode ser dada pela razão entre o seno e o cosseno desse ângulo.
Se o valor do cosseno for igual a zero, não é possível calcular essa razão. Isso acontece com os arcos de 90° (π/2 rad) e 270° ( 3π/2 rad)!
Vejamos agora qual é o sinal do valor da tangente, de acordo com a posição dos arcos no círculo trigonométrico. Primeiramente, destacamos que o eixo das tangentes é orientado em sentido crescente, de baixo para cima.
Com isso, para arcos do primeiro quadrante, os valores da tangente são positivos. Veja que, realizando o processo que descrevemos anteriormente, ao se estender o segmento que liga o centro da circunferência trigonométrica à extremidade do arco (que é a hipotenusa do triângulo retângulo associado ao arco) até o eixo das tangentes, estaremos sempre na parte positiva do eixo.
Observe a figura a seguir, em relação ao arco AN:
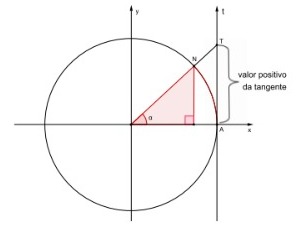
Figura 99: Valor positivo da tangente para arcos
do primeiro quadrante.