Muito bem! Agora sabemos que a qualquer arco na circunferência trigonométrica podemos associar um triângulo retângulo. Sabemos, também, que as razões
trigonométricas são definidas a partir dos lados de um triângulo retângulo, considerando-se um de seus ângulos agudos. Daí que, com o auxílio da circunferência trigonométrica, podemos calcular, portanto, as razões trigonométricas de qualquer ângulo! Vejamos como isso acontece com as três razões principais: o seno, o cosseno e a tangente.
Considere, tal como na figura a seguir, um arco AB de medida angular α na circunferência trigonométrica, e as projeções ortogonais do ponto B aos eixos x e y. Chamaremos os pontos das projeções nos eixos x e y de pontos D e C, respectivamente.
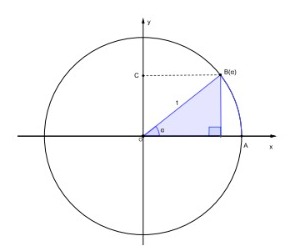
Figura 83: Triângulo retângulo associado a um arco AB em uma
circunferência trigonométrica.
BAIXAR O LIVRO EM PDF