Talvez aqui você diga: Então por que não se utiliza uma unidade de medida curva e resolve-se o problema?
Ora, mas isso é justamente o que faz a medida angular, não é? O grau e o radiano são unidades de medida curvas, são arcos de circunferência tomados como parâmetro de comparação. Logo, se quisermos uma medida do comprimento do arco em centímetros ou metros (unidades de medida linear), vamos ter que enfrentar esse problema! E é aqui que voltamos às fórmulas de comprimento da circunferência e área do círculo que apresentamos no início desta seção!
O problema da determinação do comprimento da circunferência data de tempos distantes. A fórmula C = 2.π.r é atribuída a Arquimedes (287 a.C.). Para esse cálculo, utilizou-se de um método conhecido como método da exaustão: inscrevem-se e circunscrevem-se polígonos à circunferência e, por aproximação, consegue-se definir intervalos dentre os quais esteja o comprimento da circunferência. A partir desse método, Arquimedes conseguiu aproximações também para a área de um círculo, comparando-a com as áreas de polígonos regulares inscritos e circunscritos, e relacionando-a com o comprimento da circunferência.
A ideia do método de exaustão é “simples” e genial: calcula-se a área de um círculo (e o comprimento de sua circunferência) a partir de figuras mais simples, tal como um quadrado, por exemplo. Para tanto, procura-se o maior quadrado possível inscrito (interno) ao círculo e, ao mesmo tempo, o menor quadrado possível circunscrito (externo) ao círculo. Dessa forma, a área do círculo será algum valor situado entre os valores das áreas desses dois quadrados.
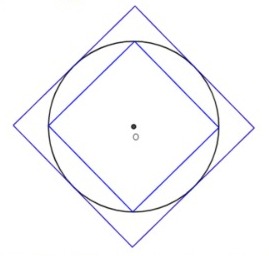
Figura 54: Quadrado inscrito e circunscrito em um círculo.