Se dividirmos, então, o valor da medida de cada lado de um triângulo qualquer pelo valor do seno do ângulo oposto ao lado considerado, encontraremos sempre as mesmas razões. No triângulo abaixo, por exemplo, cujas medidas dos lados e dos ângulos estão indicadas, veja que essas razões são, de fato, constantes:
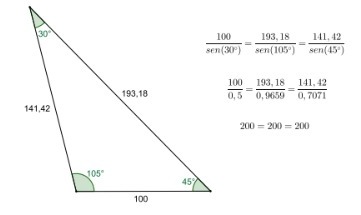
Figura 105: Exemplo de aplicação da lei dos senos.
Já a lei dos cossenos estabelece que, em qualquer triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros dois lados menos duas vezes o produto das medidas desses lados pelo cosseno do ângulo que eles formam.
Em um triângulo qualquer é possível estabelecer três relações a partir desse teorema (uma para cada lado), como mostra a figura a seguir:
Figura 106: Lei dos cossenos.
BAIXAR O LIVRO EM PDF